VAE 설명 및 구현
VAE(Varitional Auto-Encoder)란?
VAE는 생성 모델 중 하나로, 오토인코더와 비슷하게 인코더와 디코더로 구성되어 있다.
인코더로 latent space의 확률 분포를 도출하고, latent space로부터 디코딩하여 data를 생성하는 생성 모델이다.
이미지를 생성한다란?
“이미지를 생성한다”라는 것은 원하는 이미지가 나올 확률이 높은 확률분포에서 샘플링을 한다고 할 수 있다.
32 x 32 흑백 이미지가 있다고 가정하자, 하나의 픽셀은 0~255까지의 값을 가질 수 있기 때문에 흑백 이미지의 모든 경우의 수는 $256^{32\times32}$가 된다. 이 경우의 수 안에 흑백으로 표현할 수 있는 모든 이미지가 들어있을 것이다. 만약 우리가 생성하고 싶은 특정 이미지(예를 들어, MNIST 이미지)들이 있고, 해당 이미지들이 나올 가능도(likelihood)가 높은 확률분포를 안다면, 그 확률 분포에서 샘플링을 하여 이미지를 생성할 수 있을 것이다.
아래는 이해를 돕기 위해 어떤 느낌인지 표현해본 그림이다.(실제 확률분포가 저렇지는 않다.)

ELBO 구하기
우리는 주어진 이미지 데이터 x에 대해 가능도가 가장 높은 확률 분포를 알고 싶다.
즉 likelihood $p_\theta(x)$를 최대화하는 확률분포를 VAE로 근사하고 싶은 것이다.
직접 $p_\theta(x)$를 구하기 어렵기 때문에, 식을 변형하여 적분을 취해 구하려고 했지만, 고차원인 z에 대해 적분하는게 여전히 어렵기 때문에 다른 방법을 이용해야한다.
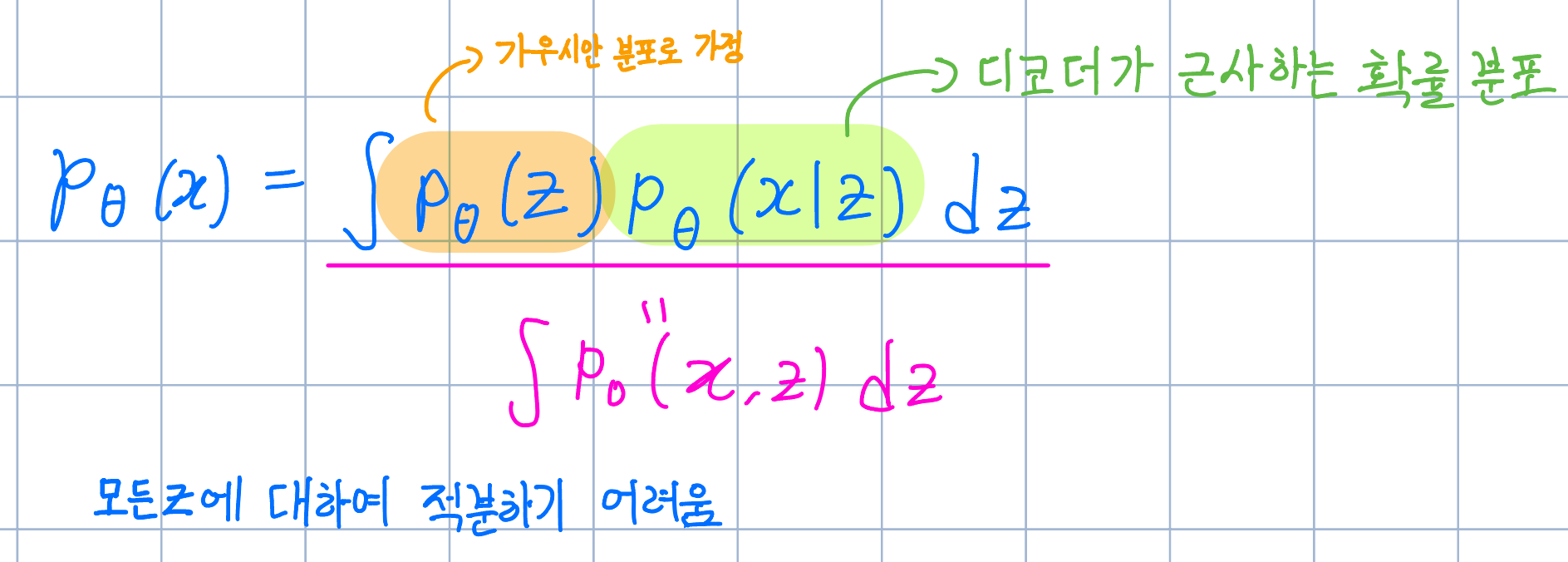
즉, 우리는$q_\phi(z|x)$(인코더로 근사하는 잠재공간 z의 확률 분포)를 이용하여 변분추론을 진행해야 하다.

Reconstrruction Error 항을 기댓값 꼴로 바꿀 수 있다.
$\int q_\phi(z|x)log(p(x|z))dz$ = $\mathbb{E}{q\phi(z|x)}[log(p\theta(x|z))]$
기댓값 꼴로 바꾼 뒤, ELBO에 -를 붙이면 해당 함수 값를 최소화하는 $\theta,\phi$를 찾는 손실함수로 정의 할 수 있다.

손실함수 정의는 완료되었으니, 이제부터는 손실함수를 실제로 어떻게 계산하는지 알아보자.
Regularization Error항 계산
우리는 p(z)가 표준 다변수 정규분포를 따른다고 가정한다.
$$p(z) \sim{N(0,I)}$$
즉, $q_{\phi}(z|x_i)$를 평균은 0이고 공분산이 단위행렬인 확률분포에 가깝게 만들어야 한다.
그래서 우리는 KL Divergence를 이용하여 두 확률분포의 차이를 표현하고 이것을 최소화하면 된다.
우리가 설계한 인코더는 x가 주어졌을 때 잠재공간 z의 평균과 표준편차를 출력하므로 이 값을 이용해 $D_{KL}$값을 계산할 수 있다.

Reconstruction Error항 계산
Reconstruction Error는 모델이 입력 데이터 x를 정확히 재구성하도록 하는 역할을 한다.
기댓값을 구하려면 적분을 해야하는데 모든 z에 대해서 적분하기는 어렵다.
그래서 적분을 하는 대신 몬테 카를로 방법을 이용하여 기댓값을 근사한다.
원래는 많은 시도를 통해 기대값을 구해야한다. 하지만 딥러닝에서 그러기에는 시간이 많이 소요되기 때문에 L=1로 설정해 랜덤하게 하나만 샘플링하여 그 값을 대표값으로 사용한다.

최종식이 아직까지 확률 분포로 되어 있기 때문에 이것을 계산하기 위해 $p_\theta(x)$가 특정한 확률분포 따른다고 가정해야한다.
여기서는 베르누이 혹은 가우시안 분포를 따른다고 가정하고 계산하고자 한다.
먼저 베르누이 분포를 따른다고 해보자.
디코더의 출력값은 x가 나올 확률 $p_i$이고, 픽셀의 수 만큼 차원 D를 가지게 된다.
각 차원의 확률을 곱으로 표현했는데, log를 이용하여 합으로 표현해줄 수 있다.
$p_\theta(x_{i,j}|z^i)$를 출력값을 이용하여 베르누이 분포로 식을 표현해준 뒤 정리하면 Cross Entropy식을 도출할 수 있다.

다음은 가우시안 분포를 따른다고 해보자.
디코더의 출력값은 $p_\theta(x_{i,j}|z^i)$의 평균과 분산이다.
$p_\theta(x_{i,j}|z^i)$를 출력값(평균과 분산)을 이용하여 가우시안 분포로 표현해준 뒤, 해당 식을 정리하면 Squared Error식을 도출 할 수 있다.

모델 구현 및 실험
import torch
import torch.nn as nn
import torchvision.datasets
import torchvision.transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import math
from torch import optim
from tqdm import tqdm
# 하이퍼파라미터 설정 값
config = {
'batch_size': 128,
'input_dim': 784,
'hidden_1_dim': 512,
'hidden_2_dim': 256,
'latent_dim': 2,
'learning_rate': 0.001,
'dropout': 0.2,
'epochs': 100
}
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# MNIST 데이터셋 다운로드 및 데이터로더 설정
train_data = torchvision.datasets.MNIST('./mnist_dataset', train=True, download=True, transform=torchvision.transforms.ToTensor())
train__dataloader = DataLoader(train_data, batch_size=config['batch_size'], shuffle=True, drop_last=True)
# VAE 모델 설계
class VAE(nn.Module):
def __init__(self, config: dict):
super(VAE, self).__init__()
self.input_dim = config['input_dim']
self.hidden_1_dim = config['hidden_1_dim']
self.hidden_2_dim = config['hidden_2_dim']
self.latent_dim = config['latent_dim']
self.dropout = config['dropout']
self.encoder = nn.Sequential(
nn.Linear(self.input_dim, self.hidden_1_dim),
nn.ReLU(),
nn.Linear(self.hidden_1_dim, self.hidden_2_dim),
nn.ReLU(),
)
# 평균과 분산을 출력하는 레이어
self.fc_mu = nn.Linear(self.hidden_2_dim, self.latent_dim)
self.fc_log_var = nn.Linear(self.hidden_2_dim, self.latent_dim)
self.decoder = nn.Sequential(
nn.Linear(self.latent_dim, self.hidden_2_dim),
nn.ReLU(),
nn.Linear(self.hidden_2_dim, self.hidden_1_dim),
nn.ReLU(),
nn.Linear(self.hidden_1_dim, self.input_dim),
nn.Sigmoid()
)
def encode(self, x):
h = self.encoder(x)
return self.fc_mu(h), self.fc_log_var(h)
def reparameterization_trick(self, mu, log_var):
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z):
return self.decoder(z)
def forward(self, x):
mu, log_var = self.encode(x)
z = self.reparameterization_trick(mu, log_var)
return self.decode(z), mu, log_var
# 손실함수 정의
def loss_function(x, x_hat, mu, log_var):
reconstruction_loss = nn.functional.binary_cross_entropy(x_hat, x, reduction='sum')
KLD = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
return reconstruction_loss + KLD
optimizer = optim.Adam(model.parameters(), lr=config['learning_rate'])
# 모델 학습 로직
model.train()
def train(config):
epochs = config['epochs']
batch_size = config['batch_size']
input_dim = config['input_dim']
print("Start training VAE...")
for epoch in tqdm(range(epochs)):
train_loss = 0
for batch_idx, (x, _) in enumerate(train__dataloader):
x = x.view(batch_size, input_dim)
x = x.to(device)
optimizer.zero_grad()
x_hat, mu, log_var = model(x)
loss = loss_function(x, x_hat, mu, log_var)
loss.backward()
train_loss += loss.item()
optimizer.step()
print("\\tEpoch", epoch + 1, "complete!", "\\tAverage Loss: ", train_loss / len(train__dataloader.dataset))
print('Finish')
train(config)
# 생성된 이미지 확인 로직
def show_images(images, num_images):
# 이미지를 (batch_size, 28, 28) 형태로 변환
images = images.view(-1, 28, 28)
# 그리드 크기 계산
grid_size = math.ceil(math.sqrt(num_images))
fig, axes = plt.subplots(grid_size, grid_size, figsize=(15, 15))
fig.subplots_adjust(hspace=0.1, wspace=0.1)
for i, ax in enumerate(axes.flat):
if i < num_images:
# 흑백 이미지로 표시
ax.imshow(images[i].cpu().numpy(), cmap='gray')
ax.axis('off')
plt.tight_layout()
plt.show()
model.eval()
def sampling_image(config):
batch_size = config['batch_size']
latent_dim = config['latent_dim']
with torch.no_grad():
noise = torch.randn(batch_size, latent_dim).to(device)
generated_images = model.decode(noise)
show_images(generated_images, batch_size)
sampling_image(config)
생성된 이미지
아래 이미지는 latent space의 차원을 2로 설정했을 때 결과이다.
전체적으로 약간 흐리게 생성되었음을 알 수 있다.

latent space의 차원이 이미지 특성을 반영하기에 너무 저차원이어서 이런 결과가 나온 것 같다는 생각이 들어 latent space 차원을 10으로 늘려서 다시 학습시켜보았다. 아래 이미지는 latent space의 차원을 10으로 설정하여 생성한 이미지이다. 2로 설정했을 때보다 비교적 선명해진 것을 확인할 수 있다. 이미지의 특성에 따라 latent space 또한 적절히 조절해야 한다는 것을 알 수 있었다.

VAE의 의의
VAE는 기존의 블랙박스와 같았던 latent space를 가우시안 분포로 근사하여, 해석 가능하고 컨트롤 가능한 형태로 변환했다는데 의미가 있다고 생각한다.
참고 자료
https://process-mining.tistory.com/161